离散事件模拟(discrete event simulation),这个东西可能在游戏领域用得并不是很多,它是模拟仿真领域的一个仿真模型,用来模拟在时间轴上一系列离散事件后,整个系统的变化情况,这么说,可能还是有点抽象,给大家举一个使用离散事件模拟的一个经典的例子,如何计算银行柜台排队的平均等待时间。
先简要描述一下这个场景,假设一个银行有两个柜台,每个柜台都可以办理业务,每隔3分钟都会有一位客户进来办理业务,如果有空的柜台,那他就直接办理,如果没有,就排队,每个人办理的业务时间都不同,可能是1~10分钟的任意一个时间,整个银行的营业时间是8小时,那请计算,在8小时所接待的所有客户中,客户的平均等待时间是多少?
这个问题,如果靠数学方法来计算,并不是很容易,那换一个思路就是,我可不可以把整个这个8小时的过程模拟一遍,把每一个客户的等待时间记录下来,然后求平均,这样就可以得到这个平均等待时间了。当然,真的把模拟的过程跑8个小时,太没有效率了,所以这个时候,就可以用离散事件模拟的方法,对这个问题去快速的进行仿真。
离散事件模拟有几个基本的概念,我们可以结合上面的这个例子来一个个看
- 时钟(Clock):整个模拟是按照时间去前进的,也就是有一个虚拟的时间去跟踪当前的时间,在这里,这个时钟就是从银行开门,一直到银行关门,总长8小时
- 结束条件(Ending Condition):模拟结束所要满足的条件,因为不可能无限模拟下去,在这里,结束条件,就是时间到了8小时
- 事件(Event):在时间轴上需要处理的事件,每个事件都有发生的时间,并且事件是按照时间的先后排列在时间轴上的,在这里,有几个事件,客户到达银行,客户结束办理业务。
整个模拟过程是怎么样的呢?简单的一句话,就是不断的从时间轴上处理一个个的事件,直至满足结束条件或者所有的事件都处理完毕。由于在相邻的两个事件与事件之间,是没有任何事情发生的,所以时钟是可以从当前的事件触发的时间直接跳到下一个事件触发的时间,这也就是“离散事件”的含义,因为这些“事件”在整个时间轴上是离散分布的,从时间的角度来看,整个模拟过程是“跳跃”前进的。
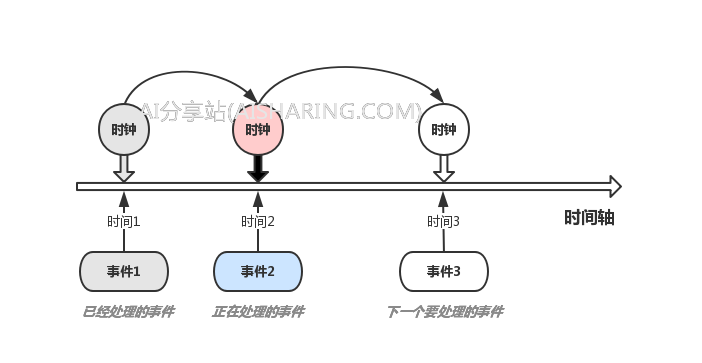
新的事件可以通过在处理老的事件的时候来不断的产生,并且添加到时间轴上,继续用上面的例子,我们把“客户n在时间t到达银行”这个事件记为E(Arrive, n, t),把“客户n在柜台m用了t分钟结束了业务办理”这个事件记为E(Finish, n, m, t),第一个事件,就是E(Arrive, Tom, 0),也就是银行一开门,来了一个用户叫Tom,这样在时间轴上,现在是这样的

这样我们初始化就好了,现在银行开门,我们开始进行8小时的模拟
我们先处理第一个事件E(Arrive, Tom, 0),当前时钟设为事件的时间,第0分钟,这个事件处理的时候,因为现在柜台是空的,所以Tom选择了1号柜台,并且需要用了8分钟办理业务,那我们就在时间轴上再添加一个时间E(Finish, Tom, 1, 8),并且,我们还需要往时间轴再添加下一个“客户到达事件”,假设3分钟后会来一个客户叫Jerry,这样时间轴上又加了一个事件E(Arrive, Jerry, 3),这个事件会加在E(Finish, Tom, 1, 8)前面,因为它会先发生
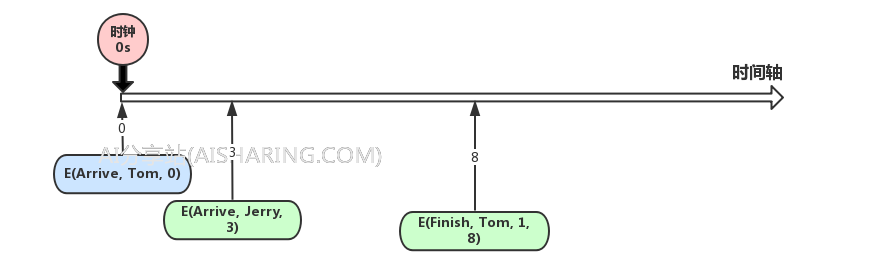
然后我们开始处理第二个事件,因为事件是按照时间轴排序的,所以我们一定能拿到一个最近要发生的事件,现在的例子里,这个事件是E(Arrive, Jerry, 3),又来了一个客户Jerry,当前时钟设为事件的时间,第3分钟,处理的过程和上面一样,不过Jerry选择2号柜台,我们会压两个事件,E(Finish, Jerry, 2, 3+6),E(Arrive, Mary, 3+3),值得注意的是,事件发生的时刻,我用了3+6这样的形式,也就是表示,当前时钟是第3分钟,这个事件需要在当前时钟的往后的6分钟发生
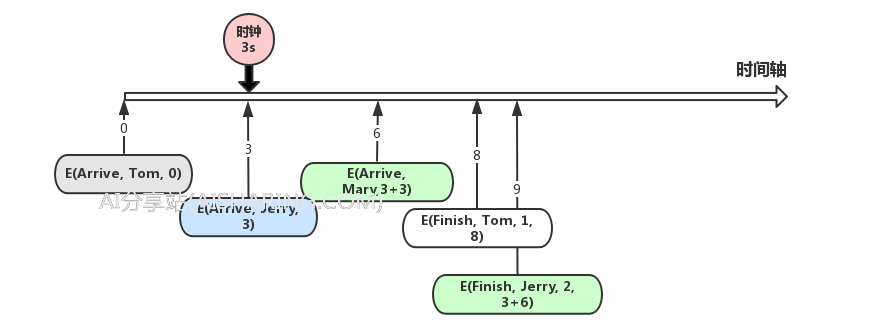
按照我们的时间轴,第三个事件,是E(Arrive, Mary, 3+3),当前时钟设为事件的时间,第6分钟,这个时候,我们不能直接为Mary添加E(Finish)事件,因为没有空的柜台,所以Mary只能选择排队,但下一个E(Arrive)事件还是需要添加
第四个事件,总算轮到很早就添加的E(Finish, Tom, 1, 8),所以添加的早,不一定执行的早,因为这个模拟是按照时间来推进的,当前时钟到了第8分钟,这个时候Tom的业务办完了,在处理E(Finish)事件的时候,我们就要去看,是不是有人在排队,如果有人在排队,那就要为排在第一个的用户,添加E(Finish)事件,现在这个人是Mary,那我们就添加E(Finish, Mary, 1, 8+6),在1号柜台,预计花6分钟的时间结束,
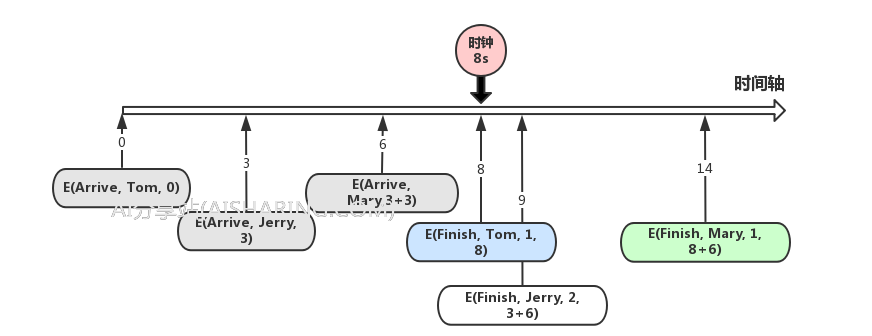
这样基本上所有可能的情况我们都简单描述了,剩下的,就是让这个模拟过程一直跑,整个过程,就是不断的有事件被处理,然后又不断的有事件产生,到最后8小时的时候,银行关门,模拟结束。基于这个模拟过程,平均等待时间就很容易算了,客户来的时间记t1(也就是处理E(Arrive)的时间点),客户开始办业务的时间记t2(也就是添加E(Finish)事件的时间点),然后t2-t1,就是单个客户的等待时间,然后把所有等待时间求和,再除以所有的客户数,就是平均等待时间了。
这个东西说起来好累,其实实现起来并不复杂,在我维护的那个TsiU的库中,已经实现了一个离散事件模拟的工具库,也就100多行代码,非常简单。在项目中,我用这个方法,做过一个工具,用来模拟在特定的同时在线数量的情况下玩家匹配游戏的平均等待时间,这样可以帮助运营人员去确定需要导入多少的用户量,来尽可能的减少匹配的等待。离散事件模拟,对于这种情景可以说是一个非常好用的利器,概念简单,实现快捷。不过在实际的游戏层面,它可不可以发挥作用呢?或者说,有没有什么游戏情景可以用这个方法去架构呢?答案是,可以有!
说了一大圈,总算到了这次分享的正题了。离散事件模拟是可以用在某些特定的游戏情境中,比如有一些游戏是战报类的,也就是说你点击了战斗之后,后台系统就已经把整个战斗的过程算好了,然后客户端就是把整个战斗结果来回放一遍,这种类型的战斗就很适合用离散事件模拟来架构(不知道类似的游戏有没有采用这样的方法),假设我们采用类似于早期最终幻想的ATB战斗系统,也就是每个参加角色都有个自己的时间条,谁先长满了就谁先行动,速度高的角色时间条长得快一点,速度低的角色时间条就长得慢一点。
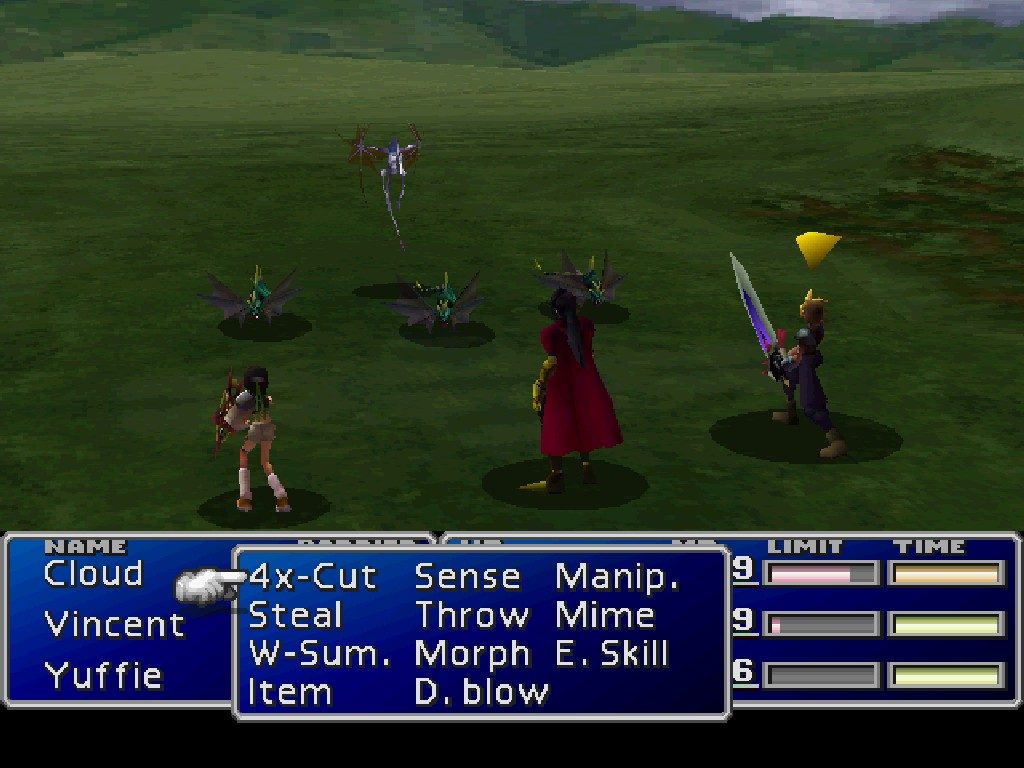
要模拟这样一场战斗就可以用离散事件模拟的结构,假设我们先简化为只能进行攻击的行动,我们就会有一个事件就是攻击,E(Attack, t),在战斗的一开始,我们把速度最快的那个人的E(Attack, t)添加到时间轴上(有点类似于上面银行的例子里,排在最前面等处理业务的那个人),然后开始进行模拟,在处理E(Attack, t)时,需要进行以下几步
- 处理伤害
- 添加下一个行动的人的E(Attack, t)
- 把自己加入行动的队列
一直进行模拟,直到己方胜出或者团灭。再复杂一点,如果再攻击中改变了时间条的增长速度,那么就需要对行动队列进行调整,也就是重新按照速度排序。这样当这场战斗模拟完毕的时候,就可以把所有的模拟过程的数据发送给客户端,由客户端进行战斗表现。
不过,在这种模拟过程中,游戏内是不能进行操作的,也就说,整个战斗是自动进行的,那如果需要支持操作,那个应该怎么处理呢?对于使用离散模拟的游戏来说,是没有办法做到“实时操作,实时生效”的,不过可以做到“实时操作,延时生效”,这在某些游戏中是很常见的,比如像类似于足球经理类的游戏,在你看比赛模拟的时候,你可以进行战术改变,换人等操作,这种操作对于玩家来说并不需要很高的实时性,只要在一段时间后能生效就可以了,再比如上面说的ATB的战斗系统,假设玩家可以在观看战斗的时候,能够使用一些全局魔法,这个时候,就可以用一些“施法时间”的概念来告诉玩家,你的施法是需要时间的,来掩盖无法实时生效的问题,但是又保证了服务器快速的模拟计算,节省服务器资源。
用离散事件模拟做“实时操作,延时生效”的关键,就是采用“分段模拟”,也就是不是一下子模拟整个过程,而是模拟一段时间,等待一段时间,再模拟一段时间,这样,如果玩家的操作发生在上一个时间段,那我就可以在下一个时间段模拟的时候,加入玩家操作的影响。
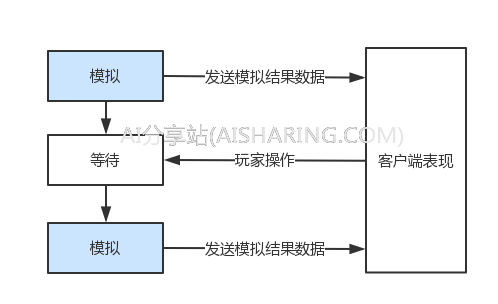
采用“分段模拟”的时候,和客户端通信会采用一段一段数据发送的方式,服务器先模拟一段时间的数据,比如模拟10秒钟逻辑,然后推送给客户端,之后等待一段时间,这段时间不能超过每段的模拟时间,一般可以等待50%~80%的模拟时间,比如等待5~8秒钟,如果等待超过10秒钟(甚至接近10秒钟),就会导致客户端那边播放完了,新的数据还没到,从而客户端的表现产生卡顿的情况,后续就一直循环这个过程,直到整个模拟结束。
离散事件模拟在游戏中虽然不是很常用,不过也是可以作为一个知识点,储备在那里,当遇到适合的场合,就可以作为选择之一加以应用。具体的例子我就不写了,大家有兴趣可以用TsiU里的那个库,自己做一个模拟银行平均等待时间的程序,来体会一下,有任何问题,和指教,欢迎讨论。
—————————————————————————————
作者:Finney
Blog:AI分享站(http://www.aisharing.com/)
Email:finneytang@gmail.com
本文欢迎转载和引用,请保留本说明并注明出处
—————————————————————————————
你说的应该就是 virtual time scheduler. 我以前看代码时见过。
离散事件模拟的话 4x游戏以及p社四萌这些游戏,核心就是这么个系统吧。【比如p社游戏就是靠事件引擎和点数堆起来的】
数学方法的部分,算是排队论中的标准模型。